编译器优化那些事儿(2):常量传播
发表于 2022/05/07
0
基础知识盘点
(1)基本块 (Basic Block) 一个基本块内的指令,处理器会从基本块的第一条指令顺序执行到基本块的最后一条指令,中间不会跳转到其它地方去,也不会有其它地方跳转到基本块的非首条指令上来。
(2)控制流图 (Control Flow Graph) 控制流图的节点是基本块,边代表基本块之间的跳转。基本块A到基本块B有一条边,表示基本块A的最后一条指令是一个跳转指令,跳转到了基本块B的第一条指令;或者基本块A的最后一条指令执行完可以顺序的走向基本块B的第一条指令。
(3)SSA (Static Single Assignment) 静态单赋值,指程序的一种表示形式,在该形式中变量只被赋值一次,如果变量需要更新,会使用一个新的变量。决定使用哪个分支处的变量,会使用Φ函数。
例如
min = a;
if(min > b)
min = b;
return min;转换为SSA形式为:
min = a;
if(min > b)
min2 = b;
return Φ(min, min2)(1)局部优化 指基本块内,跨指令的优化。
(2)全局优化 过程(函数)内的,跨基本块的优化。
(3)过程间的优化 跨过程(函数),编译单元的优化。
什么是常量传播
首先来认识一下什么是常量传播,常量传播也叫常量折叠,但有些资料中对它们的定义又是区分开来的。下面来看看它们分别是什么?
常量传播,顾名思义,就是把常量传播到使用了这个常量的地方去,用常量替换原来的变量。
x = 3;
y = 4;
z = x + y;->
x = 3;
y = 4;
z = 3 + 4;什么是常量折叠?常量折叠就是当运算符左右两边都是常数时,把结果计算出来替代原来的那部分表达式。
z = 3 + 4;->
z = 7;现在的常量传播优化技术能同时实现上面介绍的传播和折叠的功能,所以现在通常不对它们加以区分,本文后续就把常量传播和折叠统称为常量传播了。
为什么会有常量?
程序中的常量来源有3种
(1)程序员书写的,比如magic number
(2)宏定义展开后带来的,这种情况在大型工程文件中非常普遍
(3)在程序优化过程中由其它的优化技术带来的常数
为什么要进行常量传播优化?
从上面简单的例子中可以看到,常量传播可以把原本在运行时的计算转移到编译时进行,减小了程序运行时的开销。同时常量传播还有助于实现其它的优化,比如死代码消除。
如何实现?
前面介绍的常量传播的例子非常简单而且直观。如果程序的控制逻辑比较复杂时,判断一个变量是否是常数,就不是一件简单的事了,需要借助数据流的分析才能判断某个变量是否是常量。而且这个判断是保守的,即不能充分证明某个变量是常量的话就认为它是变量。这种保守的分析结果是可以接受的,因为我们优化程序的时候在性能提升与程序语义保证时优先选择保证程序语义不变。
下面我们先初步学习一下数据流分析。
数据流分析
数据流分析常常是为了实现全局优化、过程间优化,或者程序静态分析而进行的分析技术。分析得到的信息可以支撑各种优化技术的落实。
考虑下面这条指令,我们能对它做什么优化呢?
z = x + y;+ 代表各种有效的运算符, 比如+-*/等
最基本的,有下面3种假设:
(1)如果x或者y是常量,我们可以做常量传播, 用常量值替代变量x, y。如果x和y都是常量,可以在编译时刻把x+y计算出来,并赋值给z,这样就不会在运行时做这样的计算了。
(2)如果x+y在前面已经被计算过了,而且x和y再没有被赋值过(是一个可用表达式),那么此处就可以将上次计算过的值直接赋值给z, 省去再次计算的代价,这样的优化称为公共子表达式的消除。
(3)如果z从这里开始到程序结尾再没有被使用(z是不活跃变量),或者是有使用,但使用前被重新赋值了(z是不活跃变量),那么这个赋值语句是没用的,可以删除掉这条语句。
可以看到对每一种可能的优化,都需要一定的依据。这些依据就需要进行数据流的分析来获取。
下面我们介绍一下非常基础的3种数据流模式。
(1)到达定值 告诉我们在一个程序点上,过程(函数)里的变量分别是在什么位置被定值(赋值)的。常用在常量传播,复制传播上。
(2)可用表达式 告诉我们在一个程序点上,可用的表达式有哪些。常用在公共子表达式消除。
(3)活跃变量 告诉我们在一个程序点上,活跃变量(将来还会用到的变量)有哪些。常用于优化寄存器分配,删除死代码。
1. 到达定值
(1)转移函数
程序中的每一条语句都会对程序的状态产生影响,程序的状态包括了寄存器的值、内存的值、读写的文件等。对于特定的数据流分析,我们只关心对我们分析或者程序优化有用的那部分内容。比如对到达定值分析,我们只跟踪变量的定值情况,对可用表达式的分析,我们跟踪表达式的生成以及表达式分量的赋值情况,对于活跃变量我们关心变量的赋值和使用情况。
我们用转移函数来表示程序语句对程序状态的影响:

不同的分析目的,转移函数不同,对于到达定值分析,如果遇到下面的一条语句
d: u = v + w我们说这个语句生成了一个对变量u的定值d,同时杀死了其它对变量u的定值。记为:

基本块的转移函数由基本块的每一个语句的转移函数组合构成。比如2个语句组成的基本块的到达定值转移函数是

下面我们看一个具体的例子,在下面的这个流图中,每一个基本块生成的定值和杀死的定值已标记在图右侧。
图1 基本块的生成定值和杀死定值集合
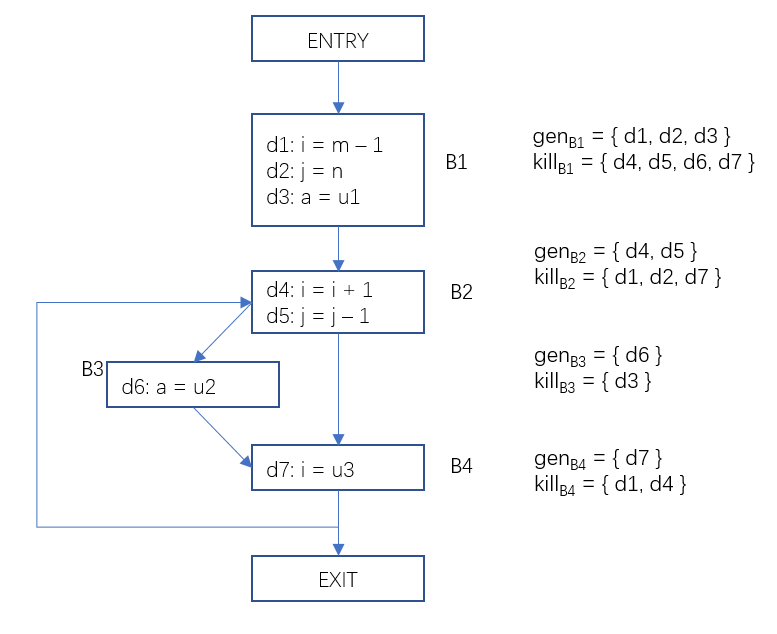
(2)数据流分析的基本思想
对每个基本块,根据输入状态,应用转移函数,求解输出状态,循环进行此操作,直到所有的基本块的输出状态不再变化为止。
(3)交汇运算(meet operator)
图2 数据流分析-交汇运算符的意义
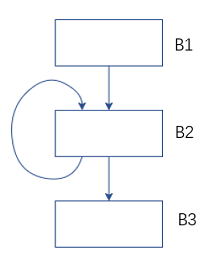
对于上面的控制流图,B2前驱节点包括B1和B2自身。B2的输入状态需要汇合B1结束后的状态OUT[B1] 和 B2结束后的状态OUT[B2], 如何汇合呢?这取决于我们的分析目的,对于到达定值分析,我们要汇集所有路径上过来的定值集合,所以对前驱节点的输出做并集运算OUT[B1]∪OUT[B2];而对于可用表达式分析,只有每一条通往此基本块的路径上都有这个表达式的生成时我们才说这个表达式在此基本块上是可用的,所以交汇运算是求交集OUT[B1]∩OUT[B2]。交汇运算用符号∧表示。
对上面的这个控制流图中的B2基本块,在第一次分析时,它自身的输出是初始化的值∅, 第二次分析时,它的输出就是上一次分析后得到输出了,就可能不再是∅了。这样迭代多次后,它的输出不再变化。当所有的基本块的输出都不再变化时,我们说这个时候到了一个定点(fix point)。
当分析达到定点时,数据流分析的结果也就得到了。
(4)到达定值分析的迭代算法

说明:此算法是非SSA表示上的到达定值分析的算法,这里用这个相对来说比较原始的算法旨在介绍它最基本的思路;如果要在SSA形式上进行到达定值分析会更加高效,前提条件是需要把程序转换为SSA形式的表示。后续介绍的活跃变量分析,可用表达式分析也是如此。
程序示例
下面我们用真实的程序对上“图1”表示的程序做到达定值分析,(这里仅列出主要的程序片段)
// 定义一个基本块的属性结构
struct N{
string name; // 基本块名称
bitset<7> gen {}; // 生成的定值
bitset<7> kill {}; // 杀死的定值
bitset<7> in {}; // 输入定值集合
bitset<7> out {}; // 输出定值集合
vector<shared_ptr<N>> pre{}; // 前驱基本块
}; // 基本块的属性和初始化
shared_ptr<N> entry, b1, b2, b3, b4, exit{};
entry = make_shared<N>(N{"entry", 0, 0, 0, 0, {}});
b1 = make_shared<N>(N{"b1", 0B0000111, 0B1111000, 0, 0, {}});
b2 = make_shared<N>(N{"b2", 0B0011000, 0B1000011, 0, 0, {}});
b3 = make_shared<N>(N{"b3", 0B0100000, 0B0000100, 0, 0, {}});
b4 = make_shared<N>(N{"b4", 0B1000000, 0B0001001, 0, 0, {}});
exit = make_shared<N>(N{"exit", 0, 0, 0, 0, {}});
// 构建基本块的前驱,形成CFG
entry->pre = {nullptr};
b1->pre = {entry};
b2->pre = {b1, b4};
b3->pre = {b2};
b4->pre = {b2, b3};
exit->pre = {b4};
// 到达定值分析过程
bool anyChange{};
vector<shared_ptr<N>> BBs{b1, b2, b3, b4, exit};
do
{
anyChange = false;
for (auto B : BBs)
{
for (auto p : B->pre)
{
B->in |= p->out;
}
auto new_out = B->gen | B->in & ~B->kill;
if (new_out != B->out)
{
anyChange = true;
}
B->out = new_out;
}
} while (anyChange);
// 输出每个基本块的输入定值,和输出定值
for (auto B : BBs)
{
cout << *B << endl;
}输出结果:
b1 0000000 1110000
b2 1110111 0011110
b3 0011110 0001110
b4 0011110 0010111
exit 0010111 0010111第一列是基本块名称,第二列是输入定值集合的位向量,第三列是输出集合的位向量。
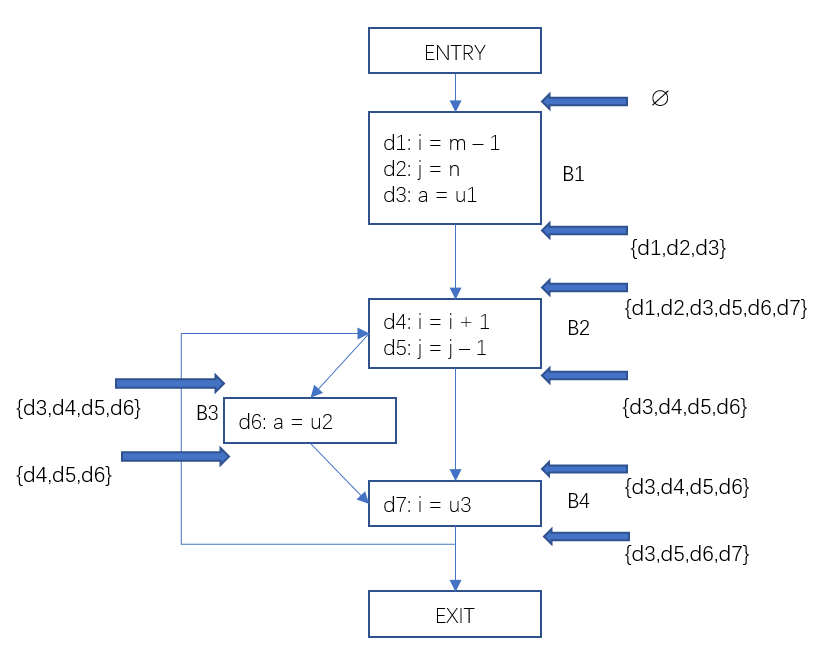
这样我们就得到了每一个基本块的输入定值集合和输出定值集合。例如对于基本块B4, 位向量<0011110>代表{d3,d4,d5,d6},是基本块开始处的到达定值集合,位向量<0010111>代表{d3,d5,d6,d7},是基本块结尾处的到达定值集合。有了这些信息就能很容易的得到在某一个程序点处p, 有哪些变量在何处被定值了。
把结果反馈到流图中如下:
图3 数据流分析-到达定值结果示例
类似的,我们用相似的方法可以进行活跃变量,可用表达式的分析。
2.2 活跃变量
一个变量x在程序点p上活跃,是说这个变量x从程序点p到程序结尾的路径上被使用,且在使用前没有对它进行新的赋值(没有被杀死)。
类似的,我们用相似的方法可以进行活跃变量,可用表达式的分析。
2. 活跃变量
一个变量x在程序点p上活跃,是说这个变量x从程序点p到程序结尾的路径上被使用,且在使用前没有对它进行新的赋值(没有被杀死)。
图4 数据流分析-活跃变量示例1
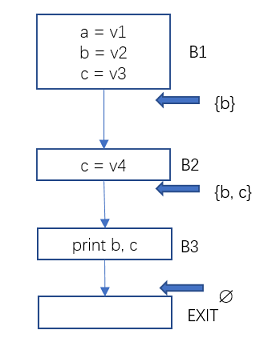
B1出口处的活跃变量只有b, 这是因为变量a再未被使用过,变量c被B2中的赋值杀死了。B2出口处的活跃变量有b和c。因为只有b和c在后面的路径中被使用,且使用前未被重新赋值。
活跃变量分析的迭代算法
活跃变量分析是一种后向分析,基本块的出口作为输入,入口作为输出。
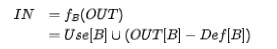
其中Use[B]表示基本块B使用了的变量, Def[B]表示基本块B赋值的变量。
迭代算法如下:

示例
图5 数据流分析-活跃变量示例2
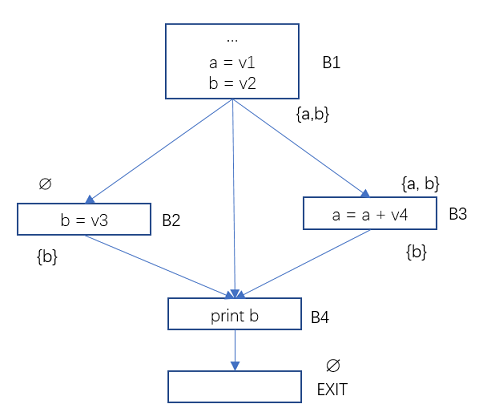
上面的程序流图中,基本块B2, B3, B4的Use和Def为:
Use[B2] = ∅, Def[B2] = {b}
Use[B3] = {a}, Def[B3] = {a}
Use[B4] = {b}, Def[B4] = ∅
3. 可用表达式
一个表达式是可用的,是说在通往程序点p的所有路径上都对那个表达式进行过计算,且计算后再未对表达式的分量进行赋值过。
图6 数据流分析-可用表达式示例1
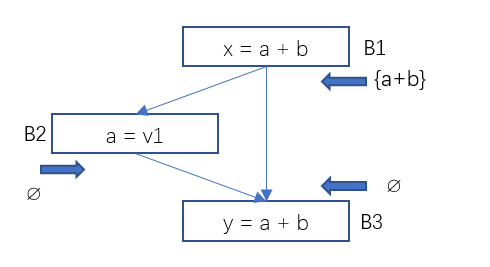
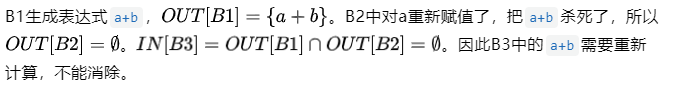
图7 数据流分析-可用表达式示例2

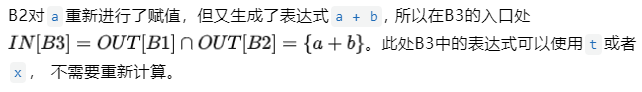
可用表达式分析的迭代算法

常量传播的数据流分析方法
前面介绍了到达定值分析,活跃变量分析,可用表达式分析。它们都是非常基础的数据流分析,在很多优化过程中会使用到这些数据流分析的结果。现在我们再次回到常量传播的优化上来。常量传播也是需要进行数据流的分析。它非常类似于到达定值,但因为常数的性质,又有所不同。
1. 常量传播使用的半格
图8 常量传播-半格
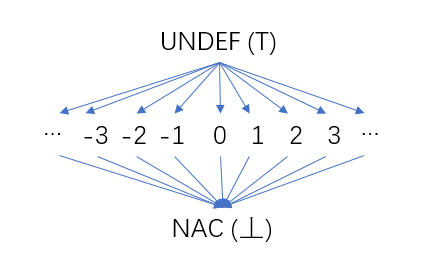
过程(函数)中的每一个变量都这样的一个半格,变量的值就是半格中的元素。在常量传播分析的初始阶段,所有的变量的值是不确定的,我们用UNDEF表示(对应格论中的最大值⊤);随着我们的分析,有些变量的值是常数,它的值就可以对应到半格的中间那一行的某一个元素,比如常数2。随着分析的进行,一些变量的值不是常数时(比如定值来自不同的前驱,每个前驱中对该变量的定值不同),用半格最底下的NAC(Not a Constant)表示(对应格论中的最小值⊥)。
前面提到过,交汇运算是对不同集合的合并。对于常量传播,每个变量的交运算(Meet Operator) 是它的不同取值在半格中的最大下界。交汇运算的规则如下:
(1)UNDEF ∧ C = C (C表示一个具体的常数)
(2)UNDEF ∧ NAC = NAC
(3)C ∧ NAC = NAC
(4)NAC ∧ NAC = NAC
(5)C ∧ C = C
(6)C1 ∧ C2 = NAC (C1≠C2)
例子:
图9 常量传播-变量映射到半格的值
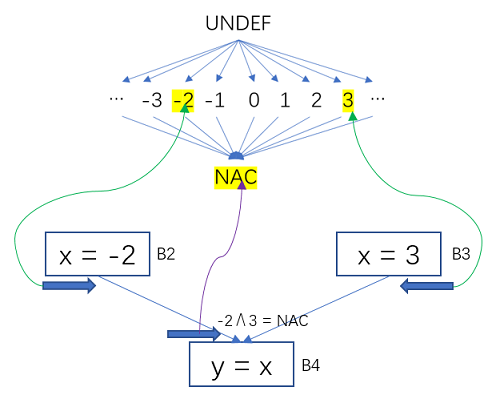
B2对x的定值为常数-2,B3对x定值为常数3,-2 ∧ 3就是在x变量的半格上取它们俩的最大下界,为NAC。
2. 常量传播的转移函数
对语句 z = x + y,转移函数如下:
x | y | z |
|---|---|---|
undef |
undef |
undef |
undef |
Cb |
undef |
undef |
NAC |
NAC |
Ca |
undef |
undef |
Ca |
Cb |
Ca + Cb |
Ca |
NAC |
NAC |
NAC |
undef |
NAC |
NAC |
Cb |
NAC |
NAC |
NAC |
NAC |
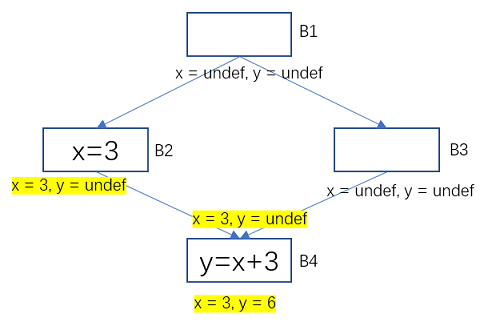
例如下面的一个流图,黄色标记表示因为程序语句的影响而发生变化的变量状态。变量x在基本块B2中的值是3, 在B3中的值是undef, 他们汇合后(最大下界)是常数3。在B4中,x是常数3, x + 3 就是常数6,所以B4中的指令就可以优化为 y = 6了。
图10 常量传播-转移函数的示例
3. 常量传播的一个简易算法
M[entry] == init
do
change = false
worklist <- all BBs; ∀B visisted(B) = false
while worklist not empty do
B = worklist.remove
visited(B) = true
m' = fB(m)
∀B' ∈ successors of B
if visited(B') then
continue
end
else
m[B'] ∧= m'
if m[B'] change then
change = true
end
worklist.add(B')
end
end
while(change == true)示例
下面的程序代码
j = 1;
x = 10;
y = 1;
while(myRead()!=0){
x = x * y;
y = y * y;
j = j + y;
}
p = j + x + y;
printf("%d\n", p);它的控制流图
图11 常量传播-示例的控制流图
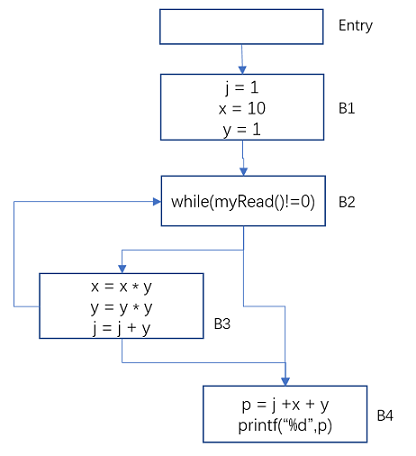
对此控制流图应用上面的算法
第一轮 <m(j),m(x),m(y),m(p)> | 第二轮 <m(j),m(x),m(y),m(p)> | 第三轮 <m(j),m(x),m(y),m(p)> | |
|---|---|---|---|
Entry |
<⊤,⊤,⊤,⊤> |
<⊤,⊤,⊤,⊤> |
<⊤,⊤,⊤,⊤> |
B1 |
<1,10,1,⊤> |
<1,10,1,⊤> |
<1,10,1,⊤> |
B2 |
<1,10,1,⊤> |
<⊥,10,1,⊤> |
<⊥,10,1,⊤> |
B3 |
<2,10,1,⊤> |
<⊥,10,1,⊤> |
<⊥,10,1,⊤> |
B4 |
<⊥,10,1,⊥> |
<⊥,10,1,⊥> |
<⊥,10,1,⊥> |
anyChange |
TRUE |
TRUE |
FALSE |
⊤表示undef, ⊥表示NAC (not a constant)
在第三轮迭代时每一个基本块的输出不再变化,到达定点。可以看出在基本块B3出口处,只有x和y是常量,分别是10和1,j和p是非常量。
基于上面的分析,上述程序可以做出如下优化
图12 常量传播-程序优化的效果

毕昇和LLVM中的常量传播
毕昇和LLVM的SCCP是一个比较高级的常量传播的pass, 它使用的算法是 Sparse Conditional Constant Propagation。
它的原理和上述的简易算法类似,有2点区别:
(1)SCCP是在SSA的表示上进行的分析。在SSA的表示上进行常量传播分析,比非SSA表示的分析要快,但得到的结果是一致的。
(2)SCCP会对条件分支中的条件进行判断,区分哪些基本块是可执行的,哪些是不可执行的,这样能够去除不可执行分支的影响,使常量传播更加准确(减少能传播但没有传播的情况)。
好了,常量传播就为大家介绍到这里。常量传播涉及到数据流的分析,所以这篇文章在介绍常量传播时也介绍了一下数据流分析,以及常见的三种数据流分析的思路。
参考文献
1. Compilers Principles, Techniques, & Tools
2. http://www.cse.iitm.ac.in/~rupesh/teaching/pa/jan17/scribes/0-cp.pdf
3. Constant propagation with conditional branches https://dl.acm.org/doi/pdf/10.1145/103135.103136


