在HPC中，MMA是指矩阵乘法与累加的融合操作，即计算D = A x B + C。其核心价值在于：

1、计算密度极高：矩阵乘法的计算量为O(M * N * K)，而数据读写量为O(M * N + M * K + K * N)，当矩阵规模较大时，计算量远大于数据传输量，属于计算密集型操作，需要发挥硬件提供的强大计算能力；

2、普适性基础操作：HPC中大量核心算法，如线性代数中的LU分解、特征值计算，深度学习中的全连接层、注意力机制等，最终都可以拆解为MMA操作，因此MMA的效率直接决定了上层应用的性能上限；

3、硬件与软件的“接口”：MMA是连接底层硬件算力与上层算法的关键桥梁，硬件设计者通过提供向量处理器、矩阵加速单元等提升MMA性能，软件开发者则通过调度使用MMA充分利用硬件算力。

综上所述，基于鲲鹏高性能CPU硬件平台，如何实现一套高效的MMA操作，对于鲲鹏HPC的发展是非常必要的。

KUPL与鲲鹏920新型号CPU硬件平台

KUPL全称鲲鹏统一并行加速库，是基于鲲鹏处理器深度优化的并行加速库，高效使能HPC各领域应用。

鲲鹏920新型号CPU硬件平台底层提供了矩阵向量化计算加速单元，给予了强大的矩阵计算能力。

在上述背景下，KUPL基于矩阵向量化计算加速单元实现矩阵编程特性模块，在屏蔽用户对于底层硬件单元感知的基础上，对外提供MMA等操作行为的模板库实现，高效使能鲲鹏硬件能力。

KUPL矩阵编程模块基础概念介绍

KUPL矩阵编程模块对外提供两类接口定义，一类是张量定义接口，包含layout、tensor等数据概念，用于描述矩阵张量的排布和数据物理内存空间；另一类是张量运算接口，通过定义tiled_mma张量乘加方法和tiled_store张量写回方法，用于后续具体张量运算；通过两类接口的搭配使用完成矩阵乘算子的编写。以下是具体基础概念介绍说明。

什么是Layout

计算机中的内存是一维的线性地址空间，而数学计算问题所要处理的空间常常是高维的。如GEMM问题的数学计算体系是二维计算空间，深度学习计算体系是三维以上的计算空间(batch, height, width, etc)。Layout即是一种高效地使用一维线性空间描述高维计算空间的方式，实现高维空间到一维空间的映射。Layout包含两个基础概念Shape和Stride，其中Shape表示多维空间的形状，Stride表示多维空间中各个维度之间数据的跨度，两者共同组成了Layout，从而完成多维空间到一维线性空间的映射。以下我们通过二维空间的Shape和Stride举例描述来进行说明：Shape: (3, 4)、Stride: (1, 3)，该Shape和Stride定义了二维空间的列优先描述：Shape中的3、4分别表示矩阵的行数和列数；Stride中的1、3分别表示元素沿着行增加1则物理存储上也相对地加1，而其中的3则表示如果元素沿着列增加1则物理存储上需要相对地加3，如下图所示：

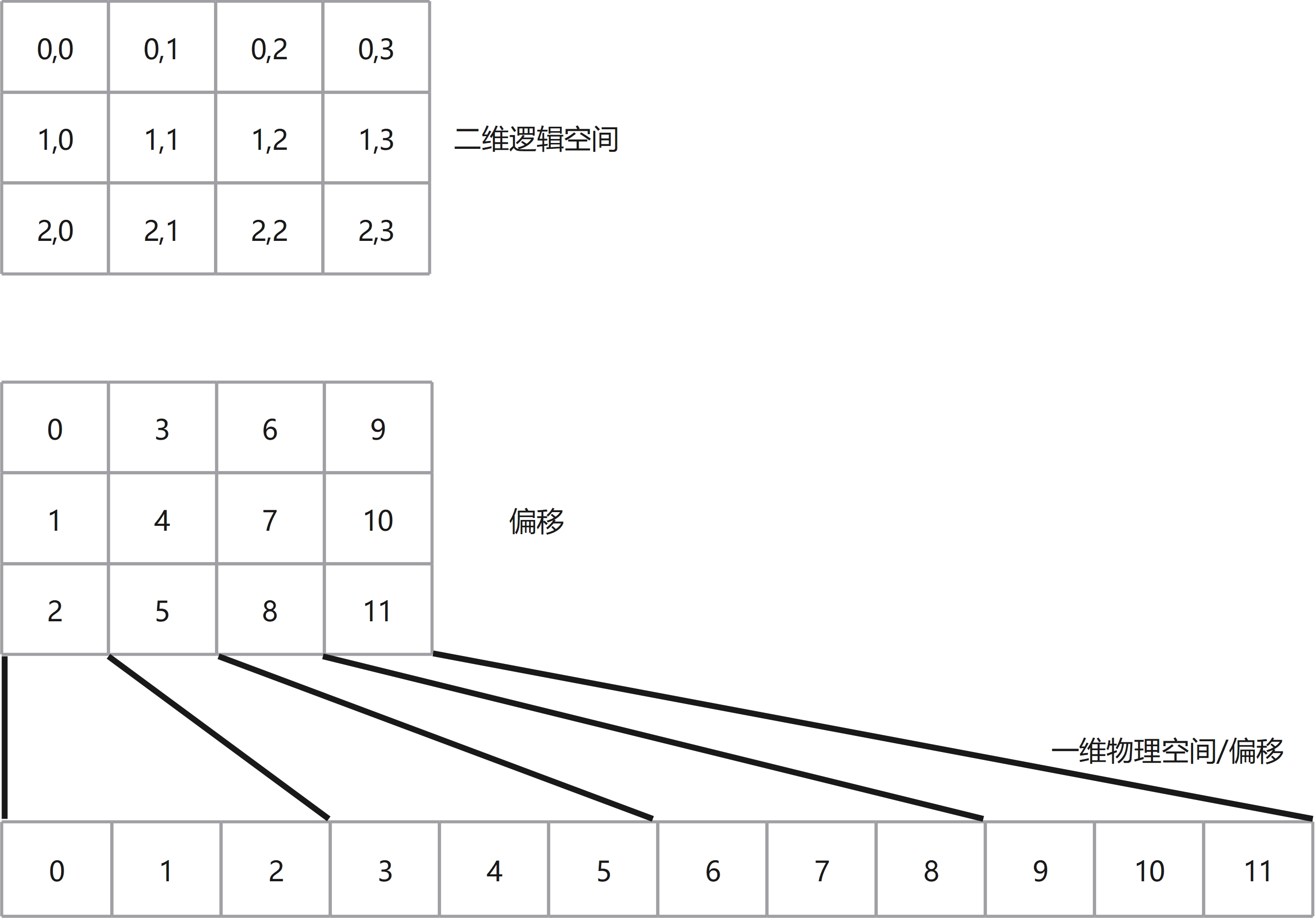
Shape:
(3, 4)、Stride: (4, 1)，和上面类似，Shape描述不变，Stride描述从(1, 3)变为(4, 1)则存储结构从列优先变为了行优先，如下图所示：

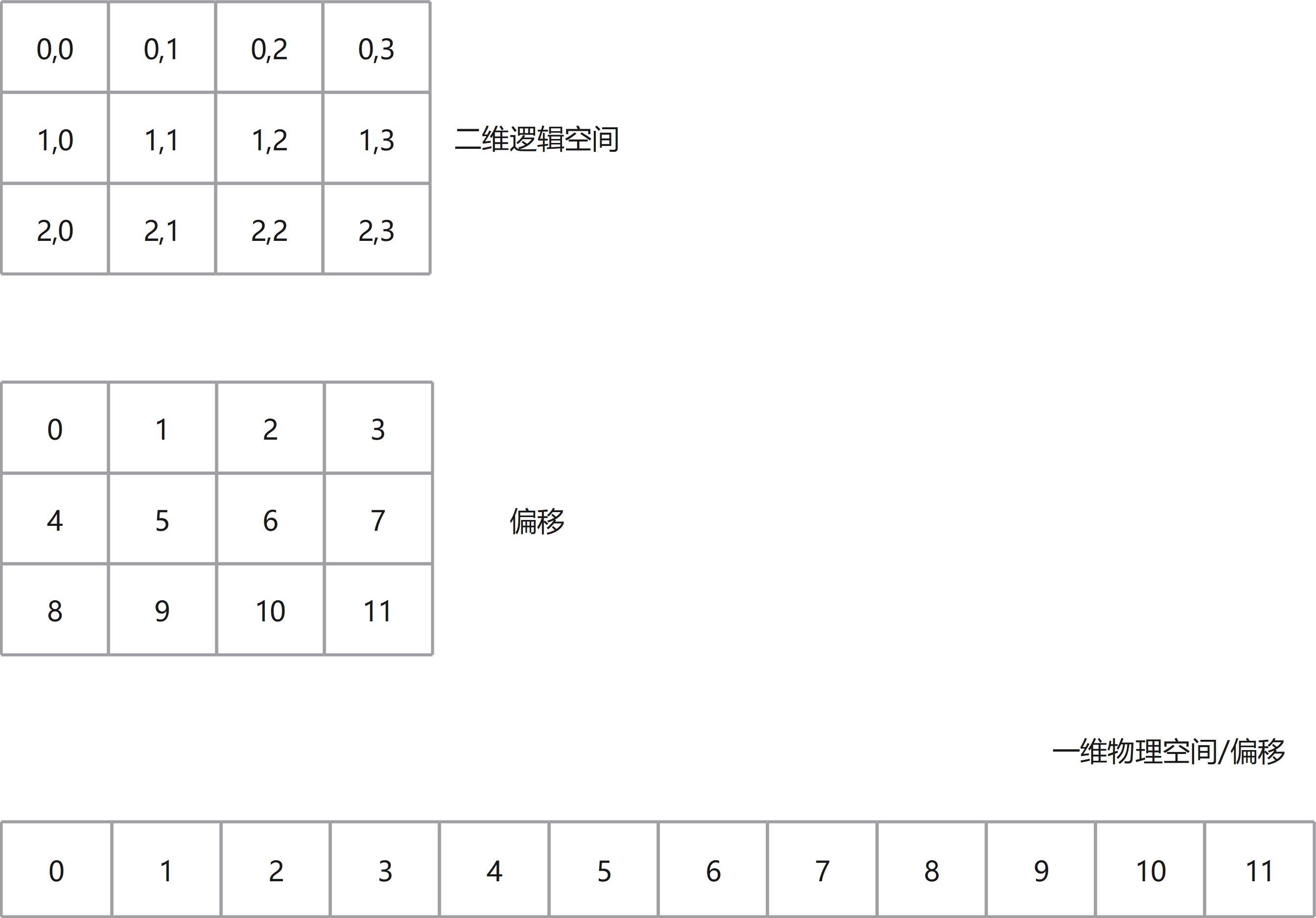
KUPL使用Layout的概念来描述矩阵的排布。

什么是Tensor

Layout描述了数据的排列和底层存储关系，但Layout并没有指定数据存储。Tensor就是在Layout的基础上包含了数据存储，即Tensor = Layout + Storage，数据存储的具体表现可以是指针表达的数据也可以是栈上的数据。在包含了数据存储后，KUPL后续MMA和Store的操作便可以对Tensor进行执行，而非直接操作用户申请数据空间。

什么是tiled_mma

tiled_mma是KUPL中用于tensor_tiled_mma接口的具体mma实现方法，其由KUPL mma_atom_ops和mma_atom_shape组合生成。

mma_atom_ops是KUPL基于鲲鹏底层矩阵向量化计算加速单元支持的矩阵乘加Size和精度实现的mma原子方法，当前支持mma_atom_ops如下列表所示：

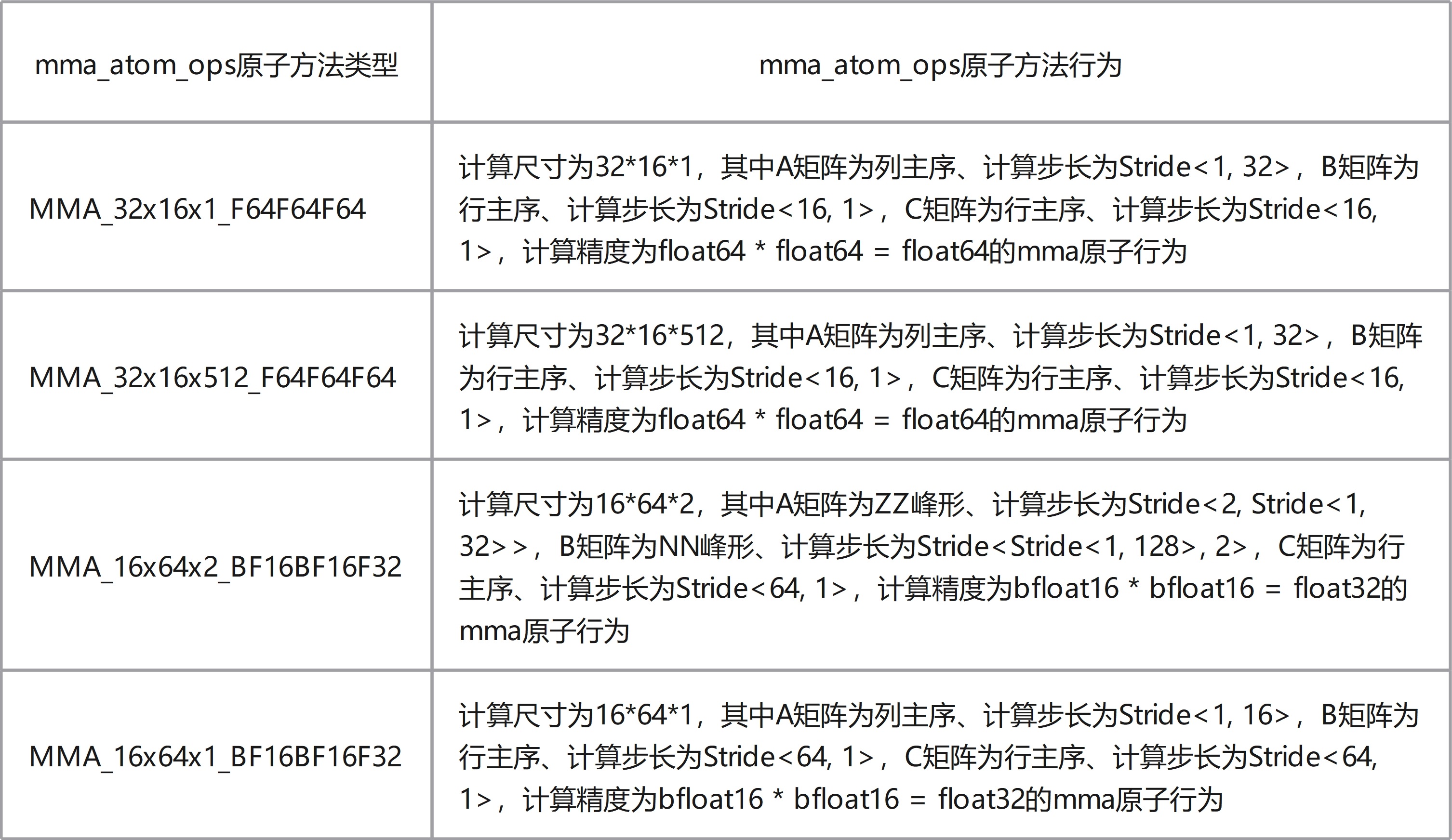
mma_atom_shape是KUPL用于扩展mma_atom_ops的Shape尺寸，其是一个三维尺寸，分别表示M/N/K计算方向上扩展的大小，基于该方式可以扩展mma_atom_ops原子方法计算的形状从而实现能力的扩展。具体扩展行为受到硬件限制，可以查看KUPL开发手册查看具体限制。

什么是tiled_store

tiled_store是KUPL中用于tensor_tiled_store接口的具体store实现方法，其由KUPL store_atom_ops和store_atom_shape组合生成。

store_atom_ops是KUPL基于鲲鹏底层矩阵向量化计算加速单元支持的存储Size和精度实现的store原子方法，当前支持的store_atom_ops如下列表所示：

store_atom_shape是KUPL用于扩展store_atom_ops的Shape尺寸，其是一个二维尺寸，分别表示M/N存储形状上扩展的大小，基于该方式可以扩展store_atom_ops原子方法存储的形状从而实现能力的扩展。具体扩展行为受到硬件限制，可以查看KUPL开发手册查看具体限制。

KUPL MMA实现float64精度32*16*512 MMA Kernel example介绍

一、定义KUPL MMA中的张量对象信息及张量运算方法

// 矩阵A/B/C的Shape形状定义
auto shape_a = make_shape(Int<32>{}, Int<512>{});
auto shape_b = make_shape(Int<512>{}, Int<16>{});
auto shape_c = make_shape(Int<32>{}, Int<16>{});

// 矩阵A/B/C的Stride步长定义
auto stride_a = make_stride(Int<1>{}, Int<32>{});
auto stride_b = make_stride(Int<16>{}, Int<1>{});
auto stride_c = make_stride(Int<16>{}, Int<1>{});

// 矩阵A/B/C的Layout排布定义
auto layout_a = make_layout(shape_a, stride_a);
auto layout_b = make_layout(shape_b, stride_b);
auto layout_c = make_layout(shape_c, stride_c);

// MMA方法和store方法定义
auto mma_atom_shape = make_shape(Int<1>{}, Int<1>{}, Int<1>{});
auto tiled_mma = make_tiled_mma(Ops<MMA_32x16x512_F64F64F64>{}, mma_atom_shape);
auto store_atom_shape = make_shape(Int<1>{}, Int<1>{});
auto tile_store = make_tiled_store(Ops<STORE_32x16_F64>{}, store_atom_shape);

二、生成tensor对象

constexpr int MATRIX_M  = 32;
constexpr int MATRIX_N  = 16;
constexpr int MATRIX_K = 512;
double *data_a = (double *)malloc(sizeof(double) * MATRIX_M * MATRIX_K);
double *data_b = (double *)malloc(sizeof(double) * MATRIX_K * MATRIX_N);
double *data_c = (double *)malloc(sizeof(double) * MATRIX_M * MATRIX_N);

// KUPL tensor对象创建
auto tensor_a = make_tensor(data_a, layout_a);
auto tensor_b = make_tensor(data_b, layout_b);
auto tensor_c = make_tensor(data_c, layout_c);

三、调用MMA方法进行计算

tensor_tiled_mma(tiled_mma, tensor_c, tensor_a, tensor_b, tensor_c);

四、调用store方法进行写回

tensor_tiled_store(tile_store, tensor_c);

总结

KUPL矩阵编程MMA旨在简化鲲鹏920新型号CPU硬件的矩阵向量化计算加速能力使能难度，从而在鲲鹏920新型号CPU上高效开发GEMM或矩阵相关融合算子，提升HPC应用性能。