基本概念与背景

基础概念

并行编程是一种通过同时执行多个计算任务来提高程序性能的编程技术。它将一个大任务分解成多个小任务，然后使用多进程或多线程在多个核上执行这些任务，从而加快整体计算速度。

在并行编程中，提升计算效率的关键包括：

任务分解：将问题划分为多个可以同时执行的子任务。

负载均衡：确保各个核的工作量大致相当，以充分利用计算资源。

通信与同步：多个核之间可能需要交换数据或协调执行顺序，以避免竞态条件或死锁。

业界总览

在上文中，我们提到任务分解和负载均衡是并行编程提升计算效率的关键。在业界，为了更好地将大任务分解为工作量相当的小任务，形成了多种模型，其中Parallel For和计算图是两种非常流行且具有代表性的模型。

Parallel For

Parallel For模型是指将一个传统的串行 for 循环的迭代次数拆分，由一个线程池中的多个线程并行执行。以下图两个数组相加为例，使用Parallel For可以将原本的串行数据加拆分成多个独立的数组元素相加，并将这些子任务分配给多个线程执行。

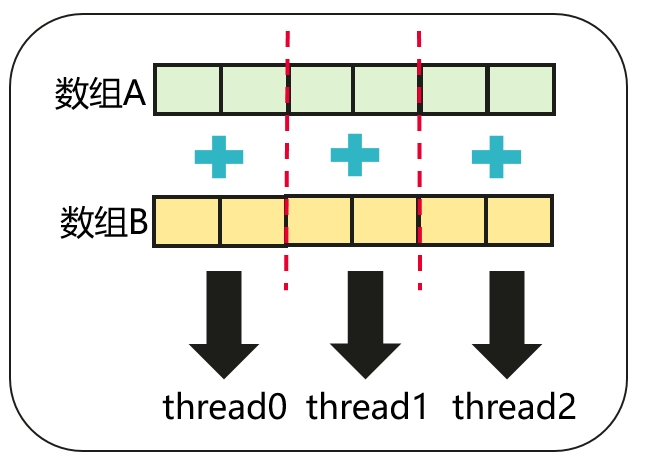
使用场景

• 循环迭代之间各元素相互独立，即任务逻辑可以通过无依赖循环的形式表达

• 每次循环迭代的任务量足够，可以抵消并行域的开销：如遍历并处理数组、列表中的大量元素。

计算图

计算图模型将程序中所需要完成的工作分解为一组任务，并明确定义这些任务之间的依赖关系。这些任务和依赖关系共同组成一个有向无环图。没有依赖关系的任务可以并行由多个线程同时执行，而依赖其他任务的任务只有当依赖的任务都执行完毕后，才会被调度执行。

以计算表达式E = A * B + C * D为例，该例子可以拆分为计算F = A * B，计算G = C * D和计算E = F + G三个任务。其中计算F = A * B任务和计算G = C * D任务之间无依赖关系，计算E = F + G则需要等到之前的两个任务均完成才能执行。上述计算步骤可构建成如下所示的计算图。

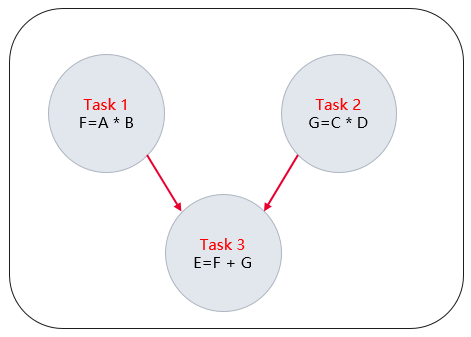
运行时系统会查看这个依赖图，它发现任务1和任务2的任务之间没有依赖关系，因此会并行执行它们。而任务3的任务被标记为等待任务1和任务2。只有当任务1和任务2都执行完毕后，任务3才会被调度执行。

使用场景

• 问题可拆分成多个任务且存在一定依赖关系

• 问题需要被反复提交执行，如HPC应用中的迭代计算

综上所述，当任务互相之间没有依赖关系，且每个任务间高度相似时，一般选用Parallel For进行并行处理；而当任务之间有显式的依赖关系时，则使用任务图处理更优。Parallel For和任务图在实际编写并行程序时均十分常用，因此如何高效地使能这两种并行编程模型在并行加速库的实现中尤为关键。

KUPL众核并行能力与与鲲鹏920新型号CPU硬件平台

KUPL全称鲲鹏统一并行加速库，是基于鲲鹏处理器深度优化的并行加速库，高效使能HPC各领域应用。鲲鹏统一并行加速库KUPL针对并行编程在任务分解、负载均衡、通信和同步方面在鲲鹏处理器上均做了不同程度的优化，从而可以更好使能鲲鹏硬件算力，提升程序性能。

KUPL众核并行编程模块集成了多种并行后端及调度策略，高效实现了上述的parallel for和任务图。其中，KUPL在任务分解和负载均衡方面进行了调整，支持二维、三维的数据的切分并辅以对应的调度策略实现负载均衡。在通信与同步方面KUPL内部并实现了与鲲鹏硬件亲和的低开销barrier从而达成鲲鹏硬件平台上通信同步的高效性。

KUPL众核并行能力example介绍

下面以数组计算d[] = a[] * b[] + c[]为例，介绍KUPL众核并行能力中的parallel for和计算图编程的使用。

Parallel for

数组计算d[] = a[] * b[] + c[]可以拆分成两个for循环，分别是计算d[] = a[] * b[]和d[] += c[]，两个循环串行执行。首先需要将这两个计算分别定义为一个函数：

// Step1：将数组操作定义成函数，函数类型符合所示要求
void axb_func(kupl_nd_range_t *nd_range, void *args, int tid, int tnum)
{
    for (int i = nd_range->nd_range[0].lower; i < nd_range->nd_range[0].upper; i += nd_range->nd_range[0].step) {
        for (int j = 0; j < i; j++) {
            d[i] += a[i] / b[i];
        }
    }
}

void d_func(kupl_nd_range_t *nd_range, void *args, int tid, int tnum)
{
    for (int i = nd_range->nd_range[0].lower; i < nd_range->nd_range[0].upper; i += nd_range->nd_range[0].step) {
        for (int j = 0; j < (N - i); j++) {
            d[i] += c[i];
        }
    }
}

之后，我们需要初始化定义所需处理的数组相加的规模，执行parallel for行为的线程数和线程组。

// Step2：初始化定义所需处理的数组相加的规模，执行parallel for行为的线程数和线程组
int num_executors = kupl_get_num_executors();
int eids[num_executors];
for (int i = 0; i < num_executors; i++) {
    eids[i] = i;
}
kupl_egroup_h eg = kupl_egroup_create(eids, num_executors);
kupl_nd_range_t range;
KUPL_1D_RANGE_INIT(range, 0, N);

之后，我们可以将上述初始化的信息填入parallel for的信息结构体中，并定义数据切分策略。其中KUPL_LOOP_POLICY_STATIC指静态策略，即编译时刻就确定了切分后任务的分配方式，而KUPL_LOOP_POLICY_DYNAMIC则为动态策略，表示此时parallel for仅对任务做切分，在运行时根据线程运行情况动态调度执行。

// Step3：将初始化定义的规模，执行parallel for行为的线程数和线程组和执行Parallel for的策略填入Parallel for的信息结构体desc中，并定义数据切分策略
kupl_parallel_for_desc_t desc = {
    .field_mask = KUPL_PARALLEL_FOR_DESC_FIELD_DEFAULT,
    .range = &range,
    .egroup = eg,
    .concurrency = num_executors,
    .policy = KUPL_LOOP_POLICY_STATIC
};

在填入了上述所有信息后，则可以调用parallel for，传入对应函数和信息结构体，实现众核并行。

// Step4：调用parallel for，传入数组相加函数task_int_loop和信息结构体desc，实现众核并行
kupl_parallel_for(&desc, axb_func, nullptr);
kupl_parallel_for(&desc, d_func, nullptr);

在函数执行完毕后，需要手动销毁创建的线程组信息。

// Step5：执行结束，销毁创建的结构体
kupl_egroup_destroy(eg);

计算图

数组计算d[] = a[] * b[] + c[]可以拆分成两个任务，分别是计算d[] = a[] * b[]和d[] += c[]，其中后一个计算任务依赖前一个计算完成。与parallel for类似，需要将这两个计算任务分别定义为一个函数：

// Step1：将数组操作定义成函数，函数类型符合所示要求
void axb_func(void *args)
{
    int *id = (int*)args;
    for (int i = (int)(1ll * (*id) * N / num_executors); i < (int)(1ll * ((*id) + 1) * N / num_executors); i++) {
        for (int j = 0; j < i; j++) {
            d[i] += a[i] / b[i];
        }
    }
}

void d_func(void *args)
{
    int *id = (int*)args;
    for (int i = (int)(1ll * (*id) * N / num_executors); i < (int)(1ll * ((*id) + 1) * N / num_executors); i++) {
        for (int j = 0; j < (N - i); j++) {
            d[i] += c[i];
        }
    }
}

在有了函数之后，我们需要定义对应的计算图。首先我们需要创建静态图。

// Step2：创建静态图
auto sgraph = kupl_sgraph_create();

之后，可以往创建的静态图上添加计算节点。下面的例子中，我们手动按照线程数切分了计算任务，将这些独立的计算任务添加到了静态图中并添加了对应的依赖，方便多个线程并行执行。

// Step3：往静态图sgraph中添加计算节点和依赖  
for (int i = 0; i < num_executors; i++) {
    kupl_sgraph_node_desc_t node_axb_desc = {
        .func = axb_func,  // 函数指针赋值
        .args = &nums[i]
    };
    auto sgraph_node_axb = kupl_sgraph_add_node(sgraph, &node_axb_desc); // 向静态图添加节点
    kupl_sgraph_node_desc_t node_d_desc = {
        .func = d_func,
        .args = &nums[i]
    };
    auto sgraph_node_d = kupl_sgraph_add_node(sgraph, &node_d_desc);
    kupl_sgraph_add_dep(sgraph_node_axb, sgraph_node_d); // 添加节点间依赖
}

在静态图信息补充完成后，需要将静态图封装成静态图任务提交至动态图执行，并等待任务执行完毕。

// Step4：将静态图封装成静态图任务提交至动态图执行，并等待任务执行完毕
auto graph = kupl_graph_create(KUPL_ALL_EXECUTORS);
kupl_sgraph_task_desc_t sgraph_desc = {
    .sgraph = sgraph
};
kupl_task_info_t task_info = {
    .type = KUPL_TASK_TYPE_SGRAPH,
    .desc = &sgraph_desc
};
kupl_graph_submit(graph, &task_info);
kupl_graph_wait(graph);

在函数执行完毕后，需要手动销毁创建的静态图和动态图。

 // Step5：销毁创建的静态图和动态图
kupl_graph_destroy(graph);
kupl_sgraph_destroy(sgraph);