基于Clang的控制流分析理论与实践
发表于 2025/12/29
0
1 概述
控制流图(Control Flow Graph, CFG)是编译器与静态分析中最基础也最关键的结构之一。不论是编译优化、静态安全分析、代码复杂度评估还是现代 IDE 的智能提示系统,都建立在 CFG 之上。
本文将从理论分析出发,全面梳理 CFG 的概念、结构、用途,以及如何在 Clang 中使用 clang::CFG::buildCFG 从源代码构造程序流图。文章最后给出简单且可复用的接口示例,帮助你在自己的工具链中轻松集成 CFG 分析。
2 控制流分析的意义
2.1 程序理解:告诉我们“代码实际怎么执行”
语法树(AST)描述的是结构,但不是执行顺序。
例如:
if (x > 0)
y = 1;
else
y = -1;AST 只会告诉你这是一条 if 语句;
CFG 则会告诉你:存在两条路径,最终会汇合。
2.2 数据流分析的基础结构
所有经典分析都基于 CFG:
- reaching definitions(可达定义)
- liveness(活跃变量)
- constant propagation(常量传播)
- dead code elimination(死代码删除)
- available expressions(可用表达式)
没有 CFG,这些分析无法表达“控制转移”导致的信息变化。
2.3 程序验证与安全分析
安全工具通过 CFG 识别:
- 未初始化变量的路径
- 越界、空指针、未检查的系统调用路径
- 异常路径、未释放资源路径
- 函数执行可能的所有路径(路径爆炸约束求解)
2.4 复杂度分析(Cyclomatic Complexity)
衡量函数复杂度的麦凯布环复杂度:
CC = E - N + 2其中 E、N 就来自 CFG。
3 控制流图(CFG)理论基础
3.1 CFG的定义
CFG = (V, E, entry, exit)
- V:基本块(BasicBlock)的集合
- E:控制转移边
- entry:入口块
- exit:出口块
一个基本块代表:
- 线性执行的语句序列(中间无跳转)
- 只有一个入口
- 只有一个出口
3.2 基本示例
- If-Else CFG:
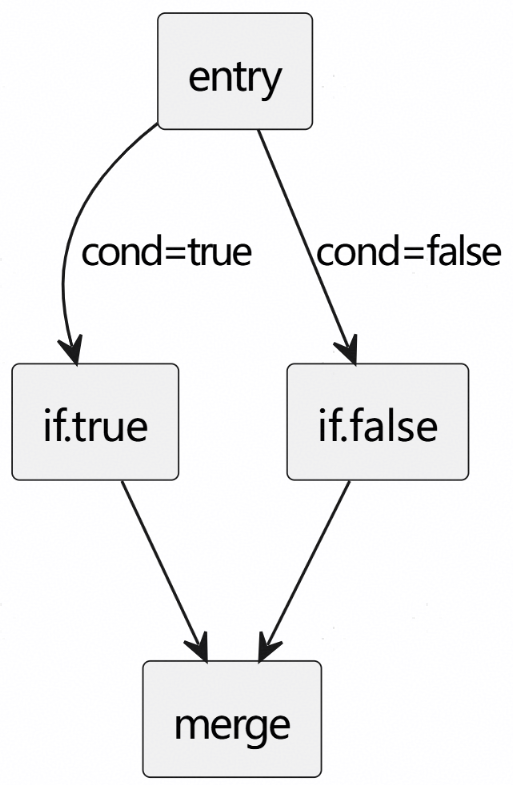
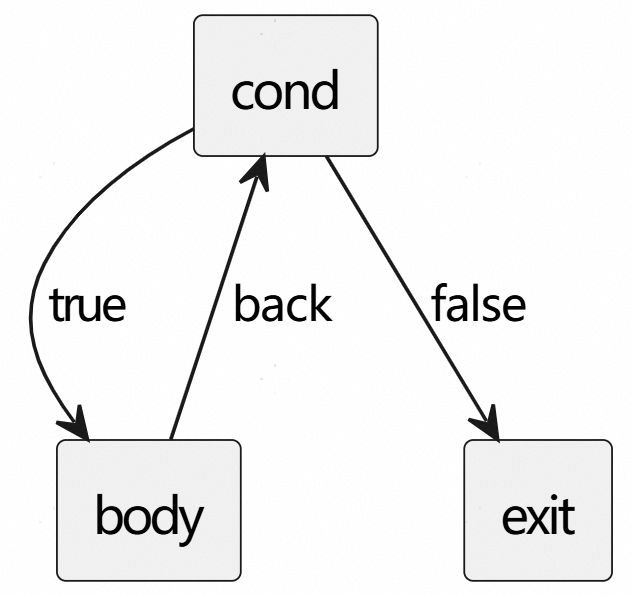
- While CFG:
4 AST vs CFG:为什么需要 CFG?
Clang 提供 AST,很多人误以为 AST 就够了。
但 AST 描述的是语法嵌套,不是控制流。
以下代码:
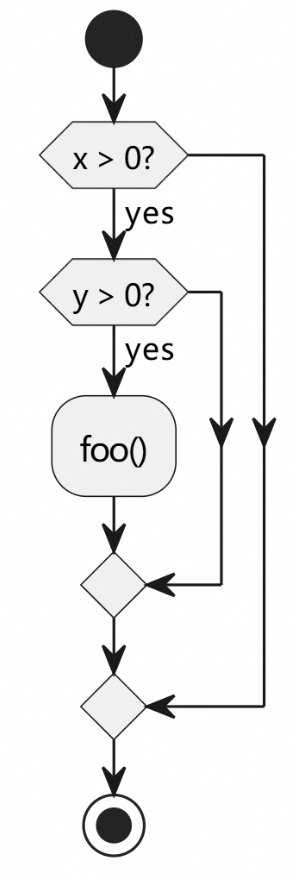
if (x > 0 && y > 0)
foo();AST:
- IfStmtBinaryOp “&&”x > 0y > 0
但这完全没体现 “短路求值”:
- 若 x <= 0,不会检查 y
- foo() 不一定执行
CFG 则明确表示了短路逻辑的路径分叉:
5 使用 Clang 构建控制流图
5.1 Clang的CFG表示
核心类:
🔸 clang::CFG
表示整张控制流图。
🔸 clang::CFGBlock
表示一个基本块:
- getBlockID()
- succ_begin() / succ_end()
- pred_begin() / pred_end()
- 可能有 Terminator(if/while/switch 等)
🔸 clang::CFGElement
块中每个语句、表达式的元素。
5.2 使用 clang::CFG::buildCFG 构建控制流图
Clang 提供一个统一接口:
std::unique_ptr<CFG> CFG::buildCFG(
const Decl *D, // 通常是 FunctionDecl
const Stmt *Body, // 函数体
ASTContext *Context,
CFG::BuildOptions BO // 构建选项
);使用流程:
FunctionDecl *FD = ...; // 你从 AST 找到的函数
ASTContext *Ctx = ...;
CFG::BuildOptions BO;
std::unique_ptr<CFG> cfg = CFG::buildCFG(FD, FD->getBody(), Ctx, BO);遍历基本块和边:
for (auto *Block : *cfg) {
int id = Block->getBlockID();
// 遍历后继
for (auto succ = Block->succ_begin(); succ != Block->succ_end(); ++succ) {
if (*succ) {
int to = (*succ)->getBlockID();
llvm::outs() << "BB" << id << " -> BB" << to << "\n";
}
}
}至此已经能把 CFG 的拓扑结构拿到手了。


