SubgraphMatching

run API

• API

  def run(dataGraph: RDD[(Long, Long)], queryGraph: Array[(Long, Long)], taskNum: Int, outputSizeLimit: Int, isIdentical: Boolean): (Long, RDD[Array[(Long, Long)]])

• 功能描述

  基于输入查询图的结构，在数据图中查找所有与查询图结构一致的子图结构，输出所有匹配结果的数量以及top K个匹配结果，输出的K个结果按照匹配结果中所有节点的度大小之和进行排序。当前算法支持两种查询模式，弱匹配与强匹配：

  弱匹配：要求数据图中的匹配结果包含查询图的结构（即查询图节点之间若不存在边连接，在数据图中并不做要求）。

  弱匹配支持的查询图结构：

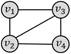
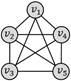
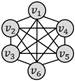
  四边形带对角线	四边形团	五边形团	六边形团

  强匹配：要求数据图中的匹配结果与查询图结构完全一致（即查询图节点之间若不存在边连接，在数据图中也需要求对应的点之间不存在边）。

  强匹配模式支持的查询图结构：

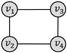
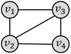
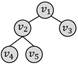
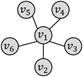
  四边形环	四边形带对角线	五节点二叉树	六节点星形

  

  二叉树和星形在强匹配过程中默认约束条件还包括：二叉树的非根和非叶子节点度需要等于3，星形的中心节点度需要等于邻居个数。

  弱匹配与强匹配模式区别示例：

  查询图结构	数据图结构	匹配模式（场景）	匹配结果数量
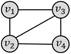
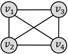
  四边形带对角线	四边形团	弱匹配（场景1.1）	6
  		强匹配（场景1.2）	0
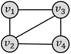
  	四边形带对角线	弱匹配（场景2.1）	1
  		强匹配（场景2.2）	1

  

  查询结果数量差异说明：

  场景1.2的查询结果为0，因为强匹配模式的规则是：“查询图中节点之间若不存在边连接，对应的数据图中也不能有边连接”；而当数据图结果为四边形团时，任意节点都有边连接，然而查询图中有两个节点之间没有边，条件不满足，所以查询结果为0。若更换数据图结果为四边形带对角线，则强匹配的约束条件满足，可以查询到一个结果（场景2.2）。

• API描述
  1. 包名：package org.apache.spark.graphx.lib.SubgraphMatching
  2. 类名：SubgraphMatching
  3. 方法名：run
  4. 输入：
     1. dataGraph: RDD[(Long, Long)]
     2. queryGraph: Array[(Long, Long)]
     3. taskNum: Int
     4. outputSizeLimnit: Int
     5. isIdentical: Boolean
  5. 参数详情：

     参数名称	参数含义	取值类型
     dataGraph	数据图边列表信息	RDD[(Long, Long)]
     queryGraph	查询图边列表信息	Array[(Long, Long)]
     taskNum	子任务数量	Int大于0的整型，推荐值1000
     outputSizeLimit	算法输出的匹配结果数量	Int大于0的整型，推荐值10000
     isIdentical	算法采用的匹配模式	Boolean型，true为强匹配，false为弱匹配

  6. 输出：
     1. Long，对应查询图在数据图上的所有匹配结果总数。
     2. RDD[Array[(Long, Long)]]，outputSizeLimit个查询结果的边列表信息，其中，每行数据为对应的查询结果边列表。
• 使用样例

  SubgraphMatching弱匹配样例：

  val sparkconf = new SparkConf().setAppName(“SubgraphMatching”).setMaster(host)
  val sc = new SparkContext(sparkconf)
  val dataEdgesRDD = sc.makeRDD(Array((1L, 2L), (1L, 3L), (1L, 4L), (1L, 5L), (2L, 3L),
  (2L, 4L), (2L, 5L), (3L, 4L), (3L, 5L), (4L, 5L)))
  val queryEdges = Array((1L, 2L), (1L, 3L), (1L, 4L), (2L, 3L), (2L, 4L), (3L, 4L))
  val partitionNum = 1
  val k = 3
  val isIdentical = false
  val (totalNum, kResults) = SubgraphMatching.run(dataEdgesRDD, queryEdges, partitionNum, k, isIdentical)
  println(“All matched number:\t%d”.format(totalNum))
  kResults.collect().map(x => (x.mkString(“\t”))).foreach(println(_))

• 样例结果：

  All matched number:5
  //前三个匹配结果信息：
  (2,3)   (2,4)   (2,5)   (3,4)   (3,5)   (4,5)
  (1,2)   (1,4)   (1,5)   (2,4)   (2,5)   (4,5)
  (1,2)   (1,3)   (1,4)   (2,3)   (2,4)   (3,4)