P?GEQRF

计算矩阵的QR分解，即。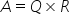

接口定义

C Interface：

void psgeqrf_(const int *m, const int *n, float*a, const int *ia, const int *ja, const int *desca, float*tau, float*work, int *lwork, int *info)

void pdgeqrf_(const int *m, const int *n, double *a, const int *ia, const int *ja, const int *desca, double *tau, double *work, int *lwork, int *info)

void pcgeqrf_(const int *m, const int *n, float _Complex *a, const int *ia, const int *ja, const int *desca, float _Complex *tau, float _Complex *work, int *lwork, int *info)

void pzgeqrf_(const int *m, const int *n, double _Complex *a, const int *ia, const int *ja, const int *desca, double _Complex *tau, double _Complex *work, int *lwork, int *info)

Fortran Interface：

PSGEQRF(m, n, a, ia, ja, desca, tau, work, lwork, info)

PDGEQRF(m, n, a, ia, ja, desca, tau, work, lwork, info)

PCGEQRF(m, n, a, ia, ja, desca, tau, work, lwork, info)

PZGEQRF(m, n, a, ia, ja, desca, tau, work, lwork, info)

参数

参数	类型	范围	说明	输入/输出
m	整型	全局	要操作的行数，比如子矩阵的行数。	输入
n	整型	全局	要操作的列数，比如子矩阵的列数。	输入
a	在psgeqrf中为单精度浮点型数组。在pdgeqrf中为双精度浮点型数组。在pcgeqrf中为单精度复数型数组。在pzgeqrf中为双精度复数型数组。	本地	调用前保存待分解的矩阵A。调用后对角线以及对角线以上的部分保存大小为min(m,n)*n的矩阵R（当m ≥ n时R为上三角矩阵），对角线以下元素和tau共同表示正交矩阵Q。	输入，输出
ia	整型	全局	子矩阵在全局矩阵中的行索引。	输入
ja	整型	全局	子矩阵在全局矩阵中的列索引。	输入
desca	整型数组	本地，全局	分布式矩阵A的矩阵描述符。	输入
tau	在psgeqrf中为单精度浮点型数组。在pdgeqrf中为双精度浮点型数组。在pcgeqrf中为单精度复数型数组。在pzgeqrf中为双精度复数型数组。	本地	初等反射的系数，长度为min(m,n)。	输出
work	在psgeqrf中为单精度浮点型数组。在pdgeqrf中为双精度浮点型数组。在pcgeqrf中为单精度复数型数组。在pzgeqrf中为双精度复数型数组。	本地	临时存储空间，退出时返回最小和最佳的lwork。	输出
lwork	整型	本地，全局	Work数组的维度。	输入
info	整型	全局	执行结果：等于0：成功。小于0：第-info个参数值不合法。	输出

依赖

#include <kscalapack.h>

#include <kscalapack_utils.h>

#include <kml_service.h>

示例

    int m = 8;
    int n = 8;       
    int nprow = 2;   
    int npcol = 2;
    int mb = 4;:q   
    int nb = 4;          
    np = 4;
    int descA[9];
    int info;
    int ipiv[10] = {0};
    int lddA = mpA > 1 ? mpA : 1;
    descinit_( descA,  &n, &n, &nb, &nb, &izero, &izero, &ictxt, &lddA, &info);

    double tau[8];
    int lwork = 48;
    double work[48];
    
    np = 4;
    /* 
     * Origin A: 
    /*  
    4.50000 11.0000 17.0000 8.00000 11.0000 11.0000 17.0000 8.00000
    14.0000 8.50000 9.00000 17.0000 14.0000 13.0000 9.00000 17.0000
    15.0000 14.0000 7.50000 11.0000 15.0000 14.0000 10.0000 11.0000
    13.0000 10.0000 15.0000 13.5000 13.0000 10.0000 15.0000 14.0000
    11.0000 11.0000 17.0000 8.00000 4.50000 11.0000 17.0000 8.00000
    14.0000 13.0000 9.00000 17.0000 14.0000 8.50000 9.00000 17.0000
    15.0000 14.0000 10.0000 11.0000 15.0000 14.0000 7.50000 11.0000
    13.0000 10.0000 15.0000 14.0000 13.0000 10.0000 15.0000 13.5000
    */
    /* Query optimal work size */ 
    pdgeqrf_(&n, &n, A,  &ione, &ione, descA, tau, work, &lwork, &info);
    * After PDGEQRF: 
    /*
    -36.3490 -31.6790 -32.1329 -35.4205 -35.1867 -31.6790 -32.1329 -35.4205
    0.342726 8.46706 11.1681 0.285094 4.34884 6.07544 11.1681 0.285094
    0.367206 0.114565 13.7477 3.02971 -0.816048 1.94287 13.2930 3.02971
    0.318245 0.245466 -0.182222 7.89794 5.36891 -0.658967 0.174397 7.86629
    0.269284 0.0337660 -0.199487 0.530335 5.89453 2.63366 -0.221784 0.0288312
    0.342726 0.111495 0.258678 -0.396869 0.304197 4.86159 0.325469 -0.0199092
    0.367206 0.114565 0.265211 0.293751 -0.0482493 -0.0280641 3.47962 0.00528634
    0.318245 0.245466 -0.182222 0.173244 -0.0665625 0.227001 -0.112593 -0.705509
    */

父主题： 矩阵分解函数