特征工程

场景介绍

特征工程指的是把原始数据转变为模型的训练数据的过程，它的目的就是获取更好的训练数据特征，使得机器学习模型逼近这个上限。大数据场景下，数据特征维度可以达到千万级别，在高维情况下，会面临维度灾难——当样本量不足时导致过拟合问题；同时，数据量过大会影响性能。以特征降维算法PCA（Principal component analysis，主成分分析）为例，经分析99%的计算耗时在于底层调用和运行SVD（Singular value decomposition，奇异值分解）算法，如果不进行SVD算法优化，会导致个性化推荐、关键对象识别、冗余信息缩减等场景的数据分析困难。因此，鲲鹏BoostKit通过优化重启技术、减少迭代轮次等优化手段，加快SVD算法的收敛速度，提升SVD算法对奇异值不分离和奇异值范围大，以及对高维数据场景的适应性。

算法原理

PCA算法
 PCA（Principal Component Analysis，主成分分析）是一种应用广泛的数据分析方法，它主要用于降维、特征提取、异常检测等方面。对矩阵A_m×n进行PCA，是指找到它的前k个主成分向量[v_1,v_2,…,v_k]，以及它对应的权重[s_1,s_2,…,s_k]。
SPCA算法
 SPCA算法（Principal Component Analysis for Sparse Matrix，稀疏矩阵主成分分析）是对稀疏矩阵进行主成分分析，它将稀疏数据从n维降低到k维（k<n），同时尽可能多的保留原始信息。
SVD算法
 SVD（Singular Value Decomposition，奇异值分解）算法是线性代数中一种重要的矩阵分解，在生物信息学、信号处理、金融学、统计学等领域，SVD都是提取信息的常用工具。在机器学习领域，它不光可以用于数据压缩、降维，还可以用于推荐系统，自然语言处理等。对矩阵A_m×n进行SVD，是指将其分解为A=USV^T，其中U_m×k叫左奇异矩阵；V_n×k是右奇异矩阵；S_k×k是奇异值矩阵，是对角矩阵，对角线上的元素称为奇异值，奇异值从大到小排列。U和V都是酉矩阵。

Covariance算法
 Covariance（协方差算法）在概率论和统计学中用于衡量两个随机变量的联合变化程度。而方差是协方差的一种特殊情况，即变量与自身的协方差。
Pearson算法
 Pearson（皮尔逊相关系数）在统计学中用于度量两个变量X和Y之间的相关程度（线性相关），其值介于-1与1之间；在自然科学领域中，该系数广泛用于度量两个变量之间的线性相关程度，+1表示完全正相关，0表示完全不相关，-1表示完全负相关。
Spearman算法
 Spearman（斯皮尔曼等级相关系数）在统计学中经常用希腊字母ρ表示，是衡量两个变量的依赖性的非参数指标，利用单调方程评价两个统计变量的相关性。如果数据中没有重复值，并且当两个变量完全单调相关时，斯皮尔曼相关系数则为+1或−1。
IDF算法
 IDF（Inverse Document Frequency，逆文档频率）是一种用于度量词语普遍重要性的方法，用以评估一个词对于一个文件集或一个语料库中的一份文件的重要程度。IDF常用于挖掘文章中的关键词，常被工业用于最开始的文本数据清洗。
DTB算法
 DTB（Decision Tree Bucket，决策树分箱）是一种基于决策树模型的数据离散化方法，是业界常见的有监督分箱方法。数据离散化是指将连续的数据进行分段，使其变为一段段离散化的区间，离散化过程也被表述成分箱的过程。离散化数值型特征，是将无限空间中有限的个体，映射到有限的空间中，有效减小后续算法的时间和空间开销。
Word2Vec算法
 Word2Vec（词向量）算法目的是将词转换为稠密向量表示（Distributed Representation），这样词之间的关系就可以用向量之间的距离来表示。除文本外，也可以用于编码类别变量，即“万物皆可Embedding”。相较于One Hot等特征编码方式，Word2Vec可以提取固定长度的稠密特征，富含更多的上下文信息，能提升下游算法的精度和性能。Spark开源Word2Vec算法不能处理词表过大的数据，迭代到收敛非常耗时，因此基于Spark的高效分布式Word2Vec算法很有意义。

编程实例

本示例以Pearson算法来介绍编程示例。

Pearson为ML API

模型接口类别	函数接口
ML API	def corr(dataset: Dataset[_], column: String): DataFrame def corr(dataset: Dataset[_],column: String, method: String): DataFrame

模型接口类别

函数接口

ML API

def corr(dataset: Dataset[_], column: String): DataFrame

def corr(dataset: Dataset[_],column: String, method: String): DataFrame

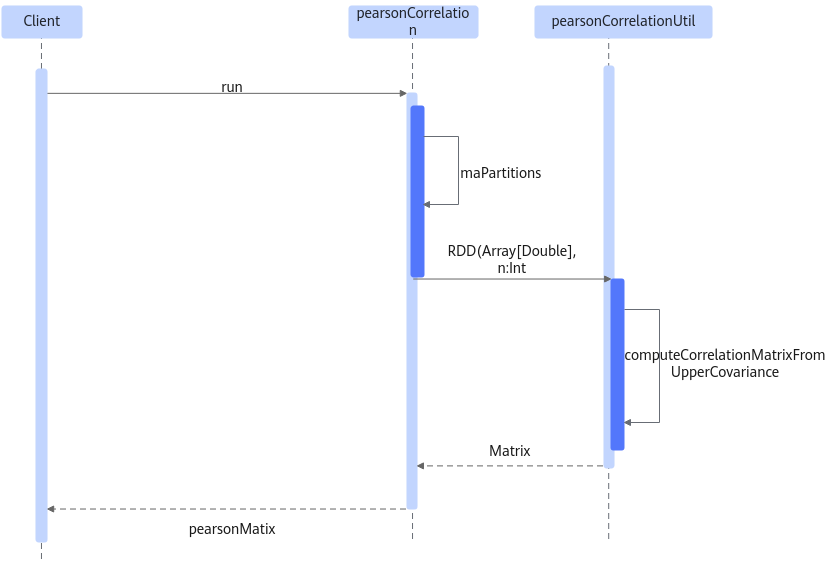
Pearson算法时序图如图1所示。

图1 Pearson算法时序图

功能描述
 传入Dataset格式的样本数据，调用fitPredict接口，输出聚类结果。

输入输出

包名：org.apache.spark.ml.stat
类名：Correlation
方法名：corr

输入：Dataset[_]，训练样本数据，必须字段如下。

参数名称	取值类型	描述
data	Dataset[Vector]	矩阵，以行为单位进行存储。
column	String	指定进行列进行相关矩阵计算。
method	String	相关矩阵方法，可以选择spearman和pearson这两种方法，默认为pearson。

基于原生算法优化的参数：

参数名称	取值类型	缺省值	描述
method	String	pearson	求解相关矩阵的方法，默认为pearson方法。

代码接口示例：

            
                 val mat = stat.Correlation.corr(data, "matrix")

输出：Pearson相关矩阵Matrix如下。

参数名称	取值类型	描述
df	DataFrame	pearson相关矩阵，列名为column+method。

使用样例

val mat = stat.Correlation.corr(data, "matrix")
val mat = stat.Correlation.corr(data, "matrix", “Pearson”)

父主题： 机器学习算法