耿贝尔分布

生成符合耿贝尔分布（gumbel distribution）的随机数向量。

接口定义

int vsRngGumbel (const int method, VSLStreamStatePtr stream, const SizeType n, float *r, const float a, const float beta);

int vdRngGumbel (const int method, VSLStreamStatePtr stream, const SizeType n, double *r, const double a, const double beta);

概率密度函数

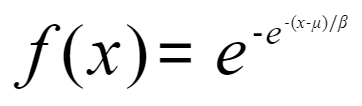
参数

参数名	类型	描述	输入/输出
method	int	随机数生成模式。 VSL_RNG_METHOD_GUMBEL_ICDF：逆累积分布函数法模式	输入
stream	VSLStreamStatePtr类型	随机数流。	输入
n	SizeType	输入输出的长度。	输入
r	在vsRngLaplace中是单精度浮点类型指针。在vdRngLaplace中是双精度浮点类型指针。	指向结果的指针。	输出
a	在vsRngLaplace中是单精度浮点类型。在vdRngLaplace中是双精度浮点类型。	运算的结果加数。	输入
beta	在vsRngLaplace中是单精度浮点类型。在vdRngLaplace中是双精度浮点类型。	运算的结果乘数。	输入

依赖

#include "krng.h"

示例

#include <stdio.h>
#include <stdlib.h>
#include "krng.h"
int main()
{
   /* initialize stream with given BRNG type and seed */
    VSLStreamStatePtr stream;
    unsigned seed = 42;
    int errcode = vslNewStream(&stream, VSL_BRNG_MCG59, seed);
    if (errcode != VSL_STATUS_OK) {
        fprintf(stderr, "Failure in newstream\n");
        return 0;
    }

    Sizetype n = 10;
    float *r = (float *)malloc(sizeof(float) * n);
    if (r == NULL) {
        fprintf(stderr, "Failure in malloc\n");
        return 0;
    }

    if (vsRngGumbel(VSL_RNG_METHOD_GUMBEL_ICDF, stream, n, r, 0.0, 1.0)) {
        fprintf(stderr, "Failure in (vsRngGumbel\n");
        goto out;
    }

    /* deinitialize the stream */
    errcode = vslDeleteStream(&stream);
    if (errcode != VSL_STATUS_OK) {
        fprintf(stderr, "Failure in deleting stream\n");
        goto out;
    }

out:
    free(r);
    return 0;
}

父主题： 高性能函数