?imatmul
矩阵缩放后in-place乘计算。
即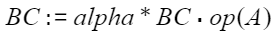 。
。
op可取值: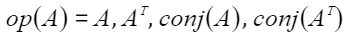 。
。
接口定义
C interface:
void cblas_simatmul(const enum CBLAS_ORDER ordering, const enum CBLAS_TRANSPOSE TransA, const BLASINT m, const BLASINT n, const float alpha, float *A, const BLASINT lda, float *BC, const BLASINT ldb);
void cblas_dimatmul(const enum CBLAS_ORDER ordering, const enum CBLAS_TRANSPOSE TransA, const BLASINT m, const BLASINT n, const double alpha, double *A, const BLASINT lda, double *BC, const BLASINT ldb);
void cblas_cimatmul(const enum CBLAS_ORDER ordering, const enum CBLAS_TRANSPOSE TransA, const BLASINT m, const BLASINT n, const float *alpha, float *A, const BLASINT lda, float *BC, const BLASINT ldb);
void cblas_zimatmul(const enum CBLAS_ORDER ordering, const enum CBLAS_TRANSPOSE TransA, const BLASINT m, const BLASINT n, const double *alpha, double *A, const BLASINT lda, double *BC, const BLASINT ldb);
Fortran interface:
CALL SIMATMUL(ORDER, TRANSA, M, N, ALPHA, A, LDA, BC, LDB)
CALL DIMATMUL(ORDER, TRANSA, M, N, ALPHA, A, LDA, BC, LDB)
CALL CIMATMUL(ORDER, TRANSA, M, N, ALPHA, A, LDA, BC, LDB)
CALL ZIMATMUL(ORDER, TRANSA, M, N, ALPHA, A, LDA, BC, LDB)
参数
参数名 |
类型 |
描述 |
输入/输出 |
|---|---|---|---|
order |
枚举类型CBLAS_ORDER |
表示矩阵是行主序或列主序。 |
输入 |
TransA |
枚举类型CBLAS_TRANSPOSE |
矩阵A为常规矩阵,转置矩阵或共轭矩阵。
|
输入 |
M |
整型数 |
矩阵op(A)、BC的行。 |
输入 |
N |
整型数 |
矩阵op(A)、BC的列。 |
输入 |
alpha |
|
表示乘法系数。 |
输入 |
A |
|
矩阵A。 |
输入 |
lda |
整型数 |
|
输入 |
BC |
|
矩阵BC。 |
输入 |
ldb |
整型数 |
|
输入 |
依赖
#include "kblas.h"
示例
C interface:
int m = 4;
int n = 3;
int lda = 4;
int ldb = 4;
float alpha = 2.0;
/**
* A:
* -0.399988, -0.211286, 0.226351,
* 0.057980, 0.185737, 0.015954,
* -0.181192, 0.092167, -0.125647,
* 0.206140, -0.441963, -0.307887
* BC:
* 0.274879, -0.184964, -0.331672,
* -0.476422, 0.318246, 0.295214,
* -0.067229, 0.314890, -0.072014,
* -0.088924, -0.222191, -0.121713
*/
float a[12] = {-0.399988, -0.211286, 0.226351,
0.057980, 0.185737, 0.015954,
-0.181192, 0.092167, -0.125647,
0.206140, -0.441963, -0.307887
};
float bc[12] = {0.274879, -0.184964, -0.331672,
-0.476422, 0.318246, 0.295214,
-0.067229, 0.314890, -0.072014,
-0.088924, -0.222191, -0.121713,
};
cblas_simatmul(CblasColMajor, CblasNoTrans, m, n, alpha, a, lda, bc, ldb);
/**
* Output BC:
* -0.219897, 0.078161, -0.150148,
* -0.055246, 0.118220, 0.009419,
* 0.024363, 0.058045, 0.018097,
* -0.036661, 0.196401, 0.074947
*/
Fortran interface:
PROGRAM IMATMUL
INTEGER :: M=4, N=3
INTEGER :: LDA=4, LDB=4
REAL(4) :: ALPHA=2.0
REAL(4) :: A(4, 3), BC(4, 3)
DATA A/-0.399988, -0.211286, 0.226351,
0.057980, 0.185737, 0.015954,
-0.181192, 0.092167, -0.125647,
0.206140, -0.441963, -0.307887/
DATA BC/0.274879, -0.184964, -0.331672,
-0.476422, 0.318246, 0.295214,
-0.067229, 0.314890, -0.072014,
-0.088924, -0.222191, -0.121713/
EXTERNAL SIMATMUL
CALL SIMATMUL('C', 'N', M, N, ALPHA, A, LDA, BC, LDB)
END
* Output BC:
* -0.219897, 0.078161, -0.150148,
* -0.055246, 0.118220, 0.009419,
* 0.024363, 0.058045, 0.018097,
* -0.036661, 0.196401, 0.074947